Your boss asked you to build a fraud detection classifier, so you’ve created one.

The output of your fraud detection model is the probability [0.0-1.0] that a transaction is fraudulent. If this probability is below 0.5, you classify the transaction as non-fraudulent; otherwise, you classify the transaction as fraudulent.
To evaluate the performance of your model, you collect 10,000 manually classified transactions, with 300 fraudulent transaction and 9,700 non-fraudulent transactions. You run your classifier on every transaction, predict the class label (fraudulent or non-fraudulent) and summarise the results in the following confusion matrix:
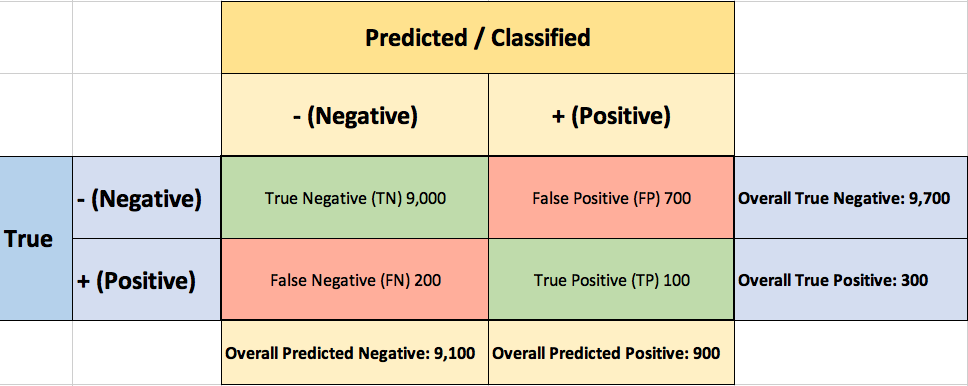
A True Positive (TP=100) is an outcome where the model correctly predicts the positive (fraudulent) class. Similarly, a True Negative (TN=9,000) is an outcome where the model correctly predicts the negative (non-fraudulent) class.
A False Positive (FP=700) is an outcome where the model incorrectly predicts the positive (fraudulent) class. And a False Negative (FN=200) is an outcome where the model incorrectly predicts the negative (non-fraudulent) class.
Asking yourself what percent of your predictions were correct, you calculate the accuracy:
Wow, 91% accuracy! Just before sharing the great news with your boss, you notice that out of the 300 fraudulent transactions, only 100 fraudulent transactions are classified correctly. Your classifier missed 200 out of the 300 fraudulent transactions!
Your colleague, hardly hiding her simile, suggests a “better” classifier. Her classifier predicts every transaction as non-fraudulent (negative), with a staggering 97% accuracy!
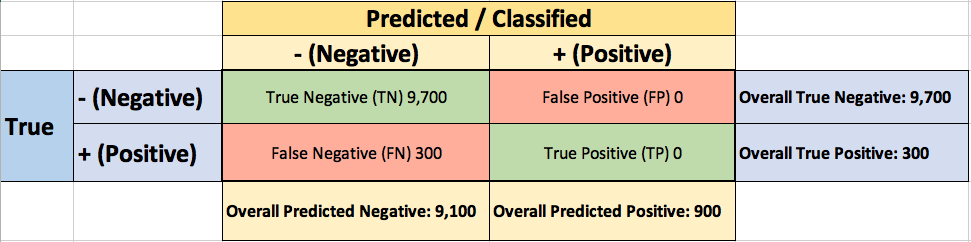
While 97% accuracy may seem excellent at first glance, you’ve soon realized the catch: your boss asked you to build a fraud detection classifier, and with the always-return-non-fraudulent classifier you will miss all the fraudulent transactions.
“Nothing travels faster than the speed of light, with the possible exception of bad news, which obeys its own special laws.”
Douglas Adams
You learned the hard-way that accuracy can be misleading and that for problems like this, additional measures are required to evaluate your classifier.
You start by asking yourself what percent of the positive (fraudulent) cases did you catch? You go back to the confusion matrix and divide the True Positive (TP – blue oval) by the overall number of true fraudulent transactions (red rectangle)
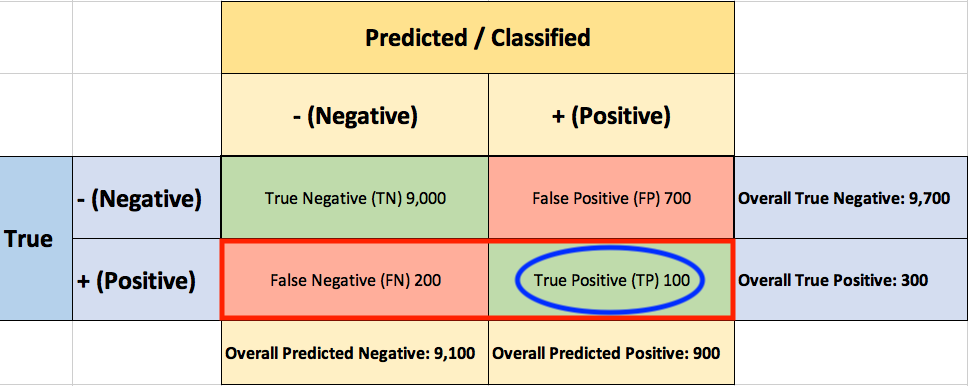
So the classier caught 33.3% of the fraudulent transactions.
Next, you ask yourself what percent of positive (fraudulent) predictions were correct? You go back to the confusion matrix and divide the True Positive (TP – blue oval) by the overall number of predicted fraudulent transactions (red rectangle)
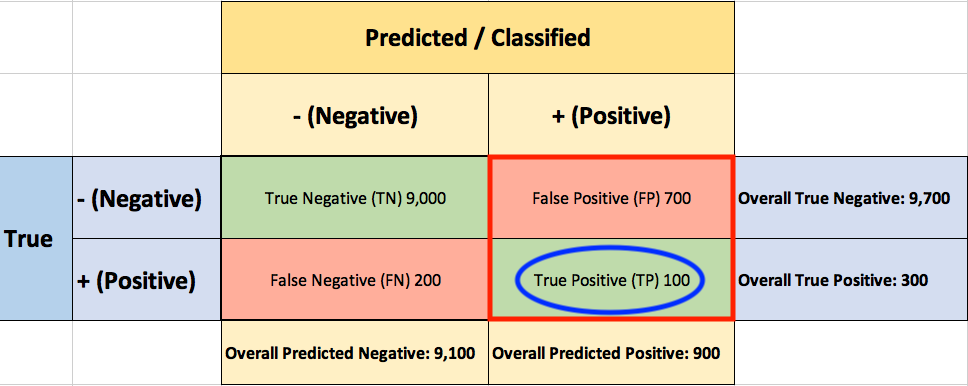
So now you know that when your classifier predicts that a transaction is fraudulent, only 12.5% of the time your classifier is correct.
F1 Score combines Recall and Precision to one performance metric. F1 Score is the weighted average of Precision and Recall. Therefore, this score takes both false positives and false negatives into account. F1 is usually more useful than Accuracy, especially if you have an uneven class distribution.
Finally, you ask yourself what percent of negative (non-fraudulent) predictions were incorrect? You go back to the confusion matrix and divide the False Positive (FP – blue oval) by the overall number of true non-fraudulent transactions (red rectangle)
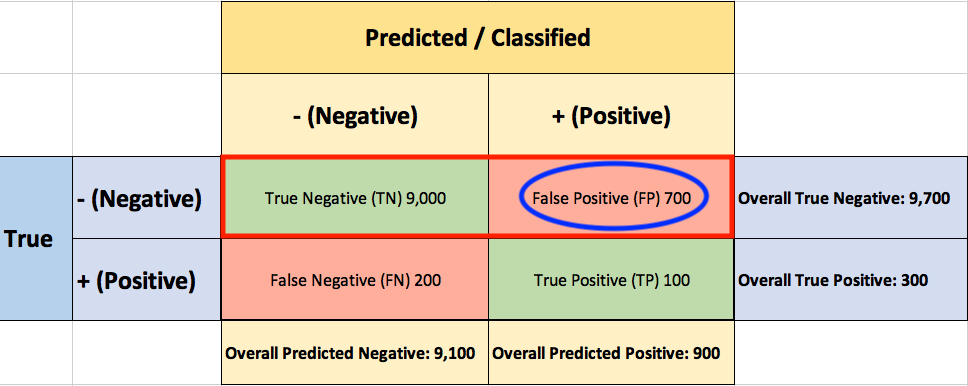
7.2% of the non-fraudulent transactions were classified incorrectly as fraudulent transactions.
ROC (Receiver Operating Characteristics)
You soon learn that you must examine both Precision and Recall. Unfortunately, Precision and Recall are often in tension. That is, improving Precision typically reduces Recall and vice versa.
The overall performance of a classifier, summarized over all possible thresholds, is given by the Receiver Operating Characteristics (ROC) curve. The name “ROC” is historical and comes from communications theory. ROC Curves are used to see how well your classifier can separate positive and negative examples and to identify the best threshold for separating them.
To be able to use the ROC curve, your classifier should be able to rank examples such that the ones with higher rank are more likely to be positive (fraudulent). As an example, Logistic Regression outputs probabilities, which is a score that you can use for ranking.
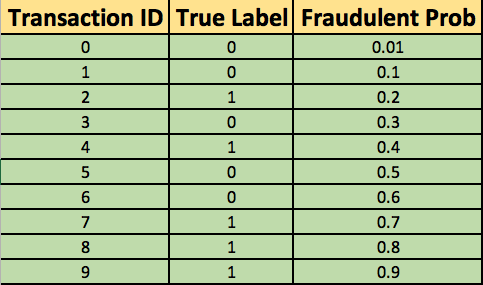
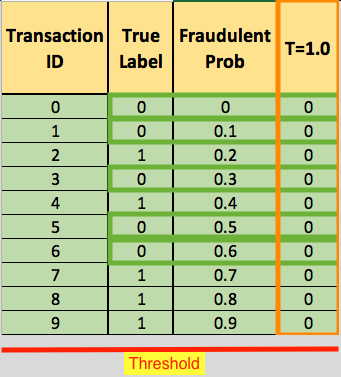
You train a new model and you use it to predict the outcome of 10 new test transactions, summarizing the result in the following table: the values of the middle column (True Label) are either zero (0) for non-fraudulent transactions or one (1) for fraudulent transactions, and the last column (Fraudulent Prob) is the probability that the transaction is fraudulent:
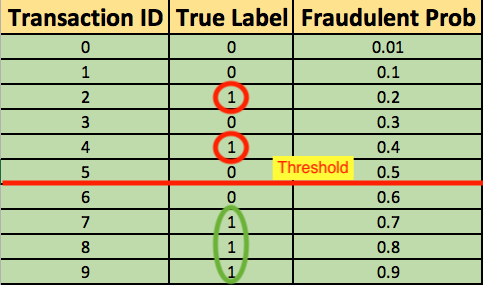
Remember the 0.5 threshold? If you are concerned about missing the two fraudulent transactions (red circles), then you may consider lowering this threshold.
For instance, you might lower the threshold and label any transaction with a probability below 0.1 to the non-fraudulent class, catching the two fraudulent transactions that you previously missed.
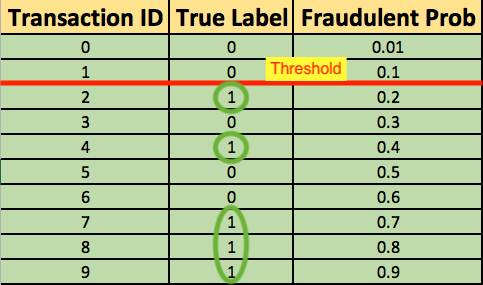
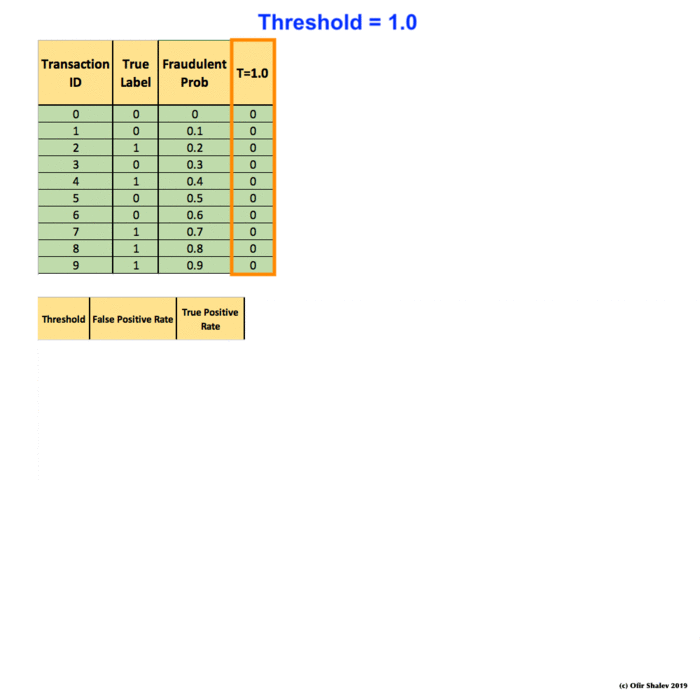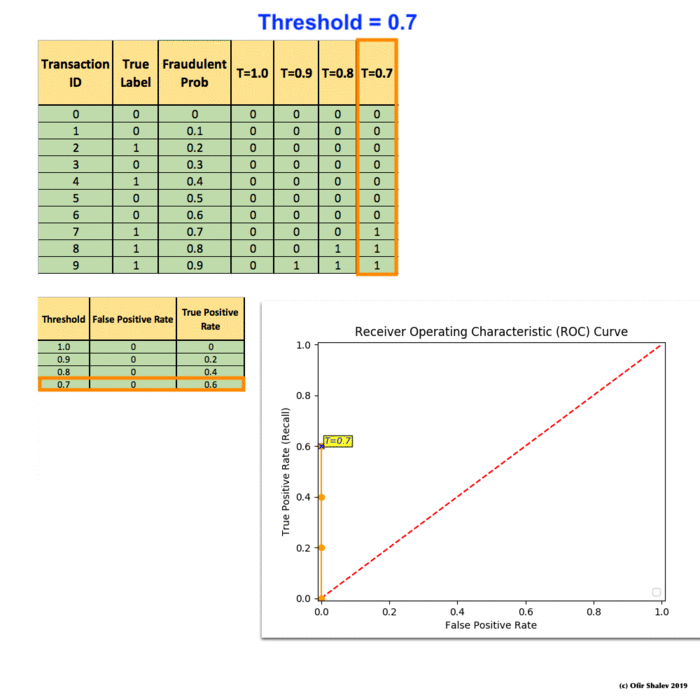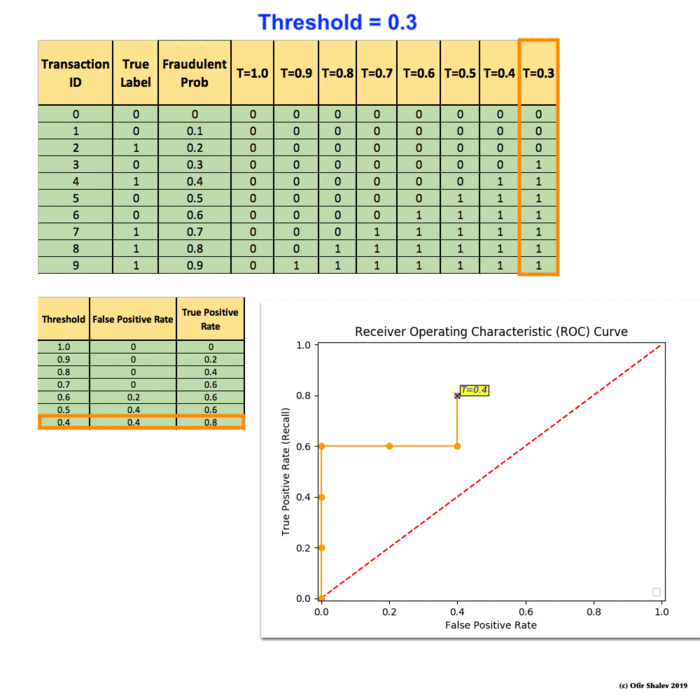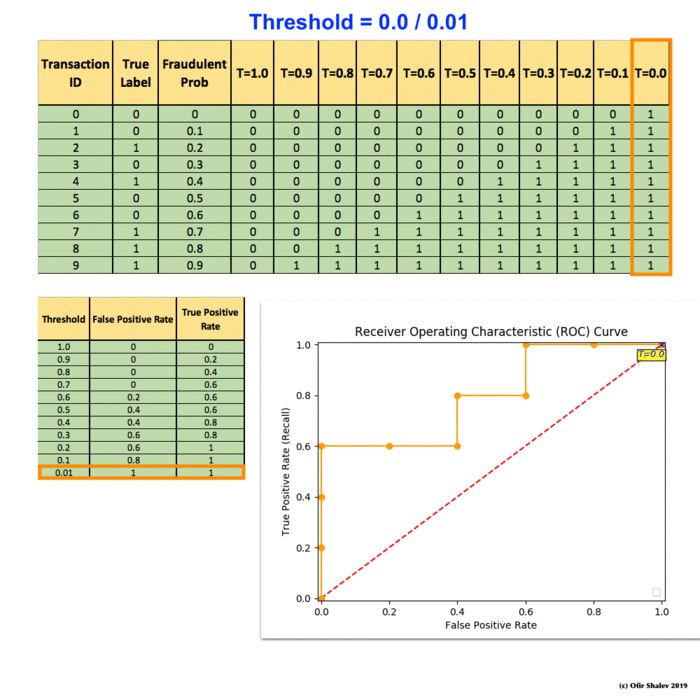
To derive the ROC curve, you calculate the True Positive Rate (TPR) and the False Positive Rate (FPR), starting by setting the threshold to 1.0, where every transaction with a Fraudulent Prob of less than 1.0 is classified as non-fraudulent (0). The column “T=1.0” shows the predicted class labels when the threshold is 1.0:
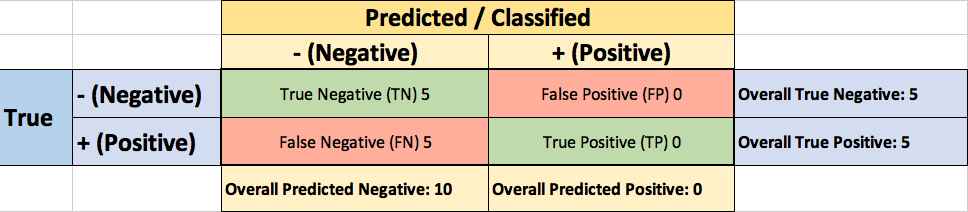
The confusion matrix for the Threshold=1.0 case:
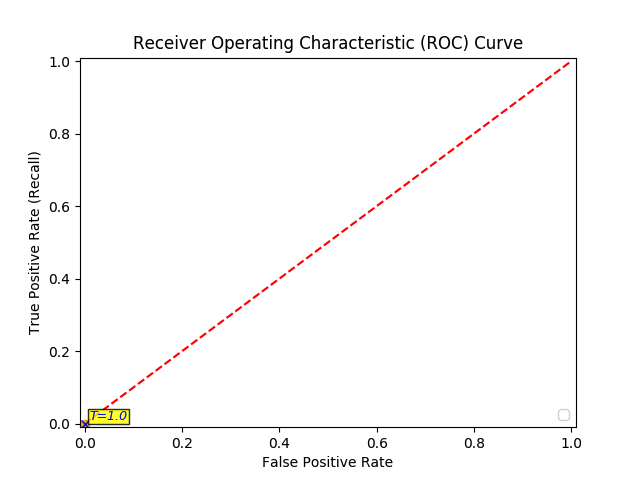
The ROC curve is created by plotting the True Positive Pate (TPR) against the False Positive Rate (FPR) at various threshold settings, so you calculate both:
You summarize it in the following table:

Now you can finally plot the first point on your ROC graph! A random guess would give a point along the dotted diagonal line (the so-called line of no-discrimination) from the left bottom to the top right corners
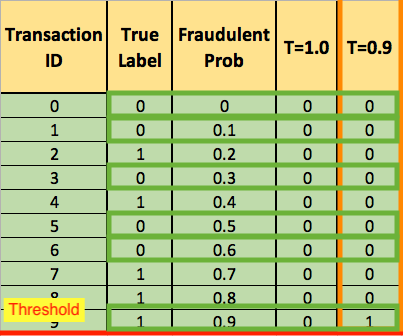
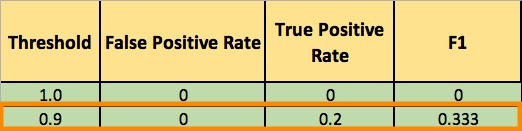
You now lower the threshold to 0.9, and recalculate the FPR and the TPR:
The confusion matrix for Threshold=0.9:
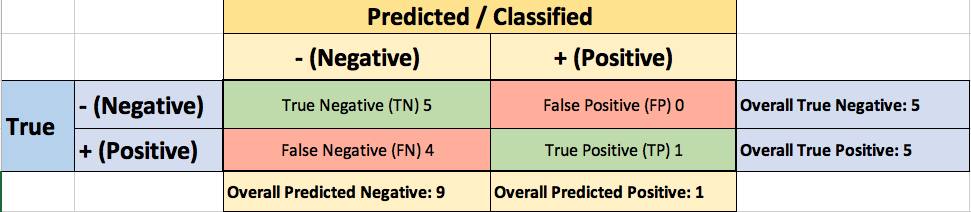
Adding a new row to your summary table:
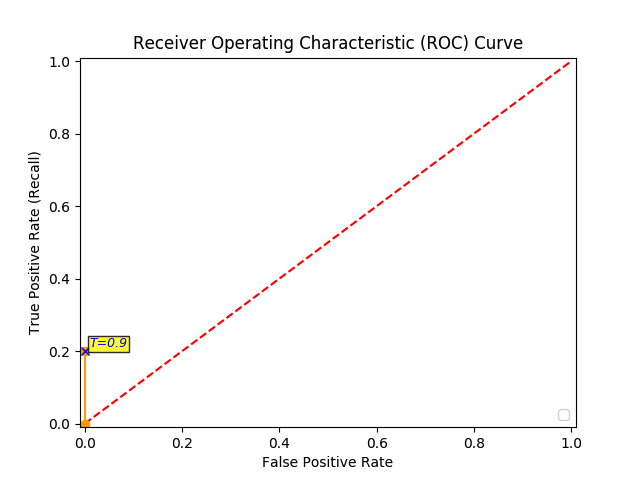
You continue and plot the True Positive Pate (TPR) against the False Positive Rate (FPR) at various threshold settings:
And voila, here is your ROC curve!
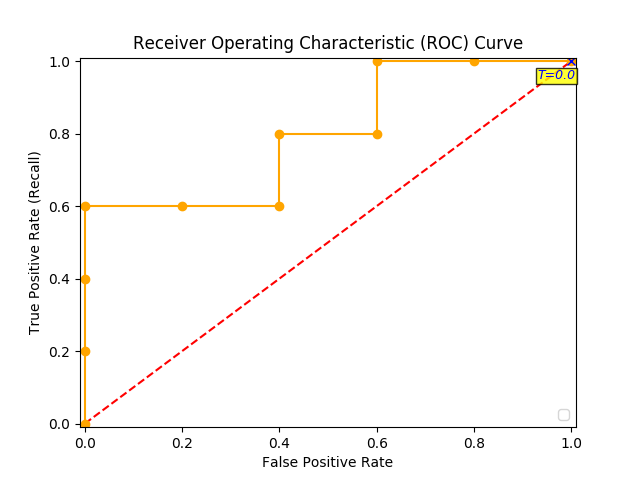
AUC (Area Under the Curve)
The model performance is determined by looking at the area under the ROC curve (or AUC). An excellent model has AUC near to the 1.0, which means it has a good measure of separability. For your model, the AUC is the combined are of the blue, green and purple rectangles, so the AUC = 0.4 x 0.6 + 0.2 x 0.8 + 0.4 x 1.0 = 0.80.
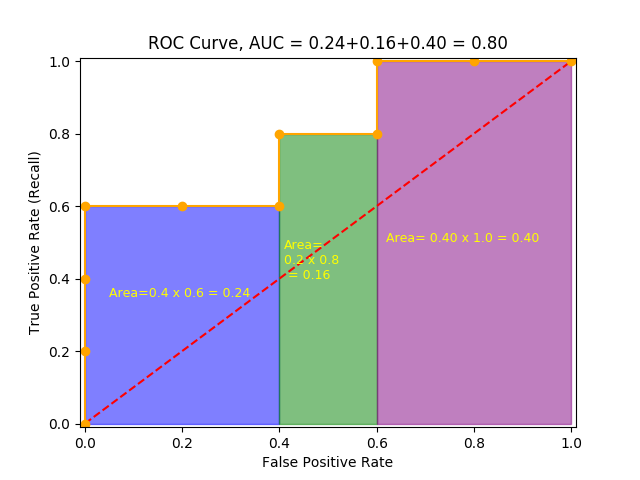
You can validate this result by calling roc_auc_score, and the result is indeed 0.80.

Conclusion
- Accuracy will not always be the metric.
- Precision and recall are often in tension. That is, improving precision typically reduces recall and vice versa.
- AUC-ROC curve is one of the most commonly used metrics to evaluate the performance of machine learning algorithms.
- ROC Curves summarize the trade-off between the true positive rate and false positive rate for a predictive model using different probability thresholds.
- The ROC curve can be used to choose the best operating point.
Thanks for Reading! You can reach me at LinkedIn and Twitter.
References:
[1] An Introduction to Statistical Learning [James, Witten, Hastie, and Tibshirani]